

Determine whether each conditional statement is true or false. For a conditional statement to be true, the hypothesis and conclusion do not necessarily both have to be true. Work with a partner: A hypothesis can either be true or false.
2.1 Conditional Statementsĭetermining Whether a Statement is True or False Polygons are plane figures made up of line segment. If ABCD is a square then it is not a rectangle. Therefore, polygon ABCD is not a rectangle. If polygon ABCD is a square, then it is a rectangle. Because it has four edges and four vertices. Squares are not trapezoids because they have two parallel sides. No, the trapezoid cannot be a square or rectangle.Ī trapezoid is a quadrilateral with at least one pair of parallel sides. Therefore, some squares are not trapezoids. Yes, all the triangles are examples of polygons the name itself tells how many sides the shape has. Reasoning and Proofs Mathematical Practicesĭecide whether the syllogism represents correct or flawed reasoning, If flawed, explain why the conclusion Is not valid.Ī triangle is the simplest form of a polygon that has three sides and three vertices.

The given sequence is not an arithmetic sequence it is a geometric sequence. \(\frac\), ………Ĭan you use the equation for an arithmetic sequence to write an equation for the sequence 3, 9, 27, 81. The nth term of the arithmetic sequence is Then find a 50.ĭ = the difference between the two numbers Write an equation for the nth term of the arithmetic sequence. Reasoning and Proofs Maintaining Mathematical Proficiency Reasoning and Proofs Cumulative Assessment – Page(120-121).Reasoning and Proofs Chapter Review – Page(116-118).2.4 – 2.6 Performance Task: Induction and the Next Dimension –.Exercise 2.6 Proving Geometric Relationships – Page(111-114).Lesson 2.6 Proving Geometric Relationships – Page(106-114).2.6 Proving Geometric Relationships –.Exercise 2.5 Proving Statements about Segments and Angles – Page(103-104).Lesson 2.5 Proving Statements about Segments and Angles – Page(100-102).2.5 Proving Statements about Segments and Angles – Page(99-104).Exercise 2.4 Algebraic Reasoning – Page(96-98).Lesson 2.4 Algebraic Reasoning – Page(92-95).2.1 – 2.3 Study Skills: Using the Features of Your Textbook to Prepare for Quizzes and Tests –.Exercise 2.3 Postulates and Diagrams – Page(87-88).Lesson 2.3 Postulates and Diagrams – Page(84-86).2.3 Postulates and Diagrams – Page(83-88).Exercise 2.2 Inductive and Deductive Reasoning – Page(80-82).Lesson 2.2 Inductive and Deductive Reasoning – Page(76-79).2.2 Inductive and Deductive Reasoning – Page(75-82).Exercise 2.1 Conditional Statements – Page(71-74).Lesson 2.1 Conditional Statements – Page(66-70).2.1 Conditional Statements – Page(65-74).Reasoning and Proofs Mathematical Practices –.Reasoning and Proofs Maintaining Mathematical Proficiency –.All you have to do is hit the links you wish to practice and solve the problems.
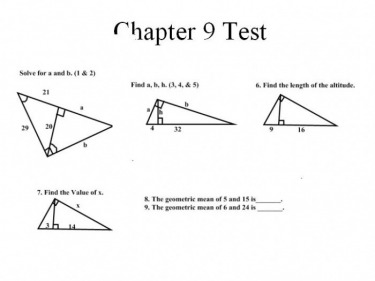
BIG IDEAS MATH GEOMETRY ANSWERS CHAPTER 9 FOR FREE
Thus Download Big Ideas Math Book Geometry Chapter 2 Reasoning and Proofs Solution Key for free of cost to kickstart your preparation for the exams.
Our Big Ideas Math Geometry Answers Chapter 2 Reasoning and Proofs will become a bridge to success. Big Ideas Math Book Geometry Answer Key Chapter 2 Reasoning and Proofsįind step-by-step solutions from Big Ideas Math Geometry Chapter 2 Reasoning and Proofs Answer Key. The Big Ideas Math Book Geometry Answer Key Ch 2 Reasoning and Proofs cover the Questions from Lessons, Exercises, Cumulative Assessments, Review Tests, Chapter Tests, and so on. With the help of Big Ideas Math Answers Geometry Ch 2 Reasoning and Proofs the students can complete homework and assignments on time.īy Solving the BIM Geometry Ch 2 Reasoning and Proofs Textbook Questions from our page you can understand the Reasoning and Proofs concept in depth in a simple manner. This is the right destination for you to practice Geometry Concepts from Big Ideas Math Geometry Answers.
BIG IDEAS MATH GEOMETRY ANSWERS CHAPTER 9 PRO
Wanna become a Pro in Maths? If your answer is yes, then you are in the right place.


 0 kommentar(er)
0 kommentar(er)
